Question 7

Question

State the Heine-Borel theorem. Proof?

Answer

Heine-Borel

The Heine-Borel theorem states that if there is a subset $A\subset {\mathbb{R}}^n$.
Then $A$ is compact, if and only if, $A$ is closed and bounded.

Proof

For $\Rightarrow$

$A$ is closed since ${\mathbb{R}}^n$ is Hausdorff and $A$ is compact

It is bounded since we can cover it by finitely many balls.

For $\Leftarrow$

Assume first that $A$ is an $n$-cube with boundary included, and say that $A$ is not compact.

If an open cover of $A$ has no finite subcover, then by halving sides of cubes we get sequences of cubes contained in each other, each having no finite subcover.

The centres of these cubes form a Cauchy sequence with a limit $x\in A$.

$d(x_n,x_m)<\epsilon ,\forall n,m>N$
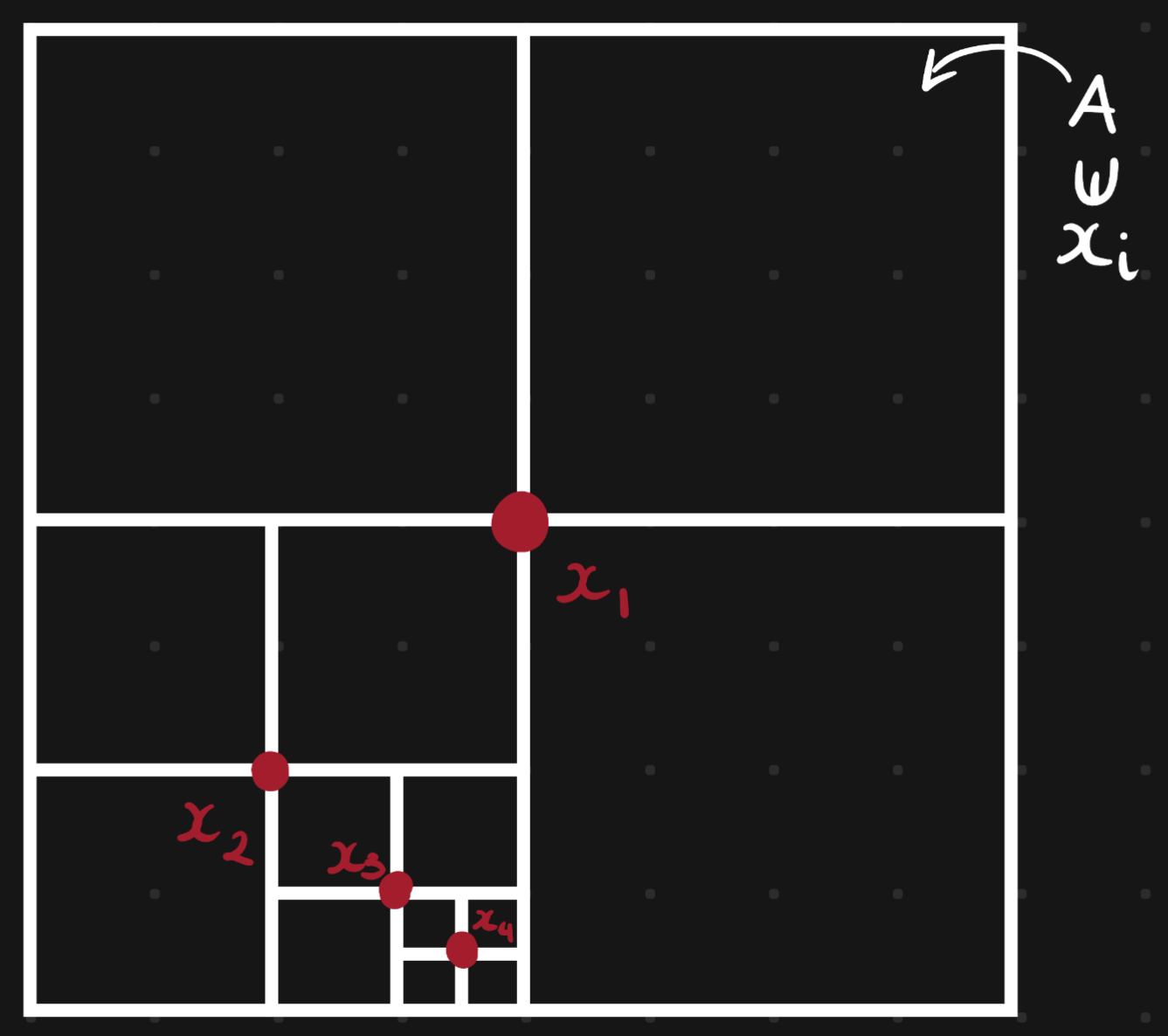
Now we have to show that $R^n$ is complete.

Any neighbourhood of $x$ from the cover will contain a small enough cube.

However, this will be a finite subcover, which is a contradiction.

QED.